全面攻略：AI脚本在迷宫寻路中的应用与优化策略解析
在数字化时代人工智能技术的飞速发展已经渗透到各个领域其中迷宫寻路疑问一直是领域内的经典难题。本文将深入探讨脚本在迷宫寻路中的应用，以及怎么样通过优化策略加强寻路效率。咱们将从脚本寻路的基本原理出发，逐步解析其在迷宫寻路中的实际应用，并探讨怎么样通过算法优化来提升寻路速度和准确性，帮助读者全面掌握脚本在迷宫寻路中的技巧与策略。
### 一、脚本寻路原理及在迷宫寻路中的应用
迷宫寻路疑惑本质上是一个路径搜索难题，而脚本寻路则通过模拟人类寻路表现，利用预设的规则和算法来寻找最短路径。下面我们将详细介绍脚本在迷宫寻路中的应用及其原理。
#### 脚本寻路迷宫攻略大全
脚本在迷宫寻路中的应用首先需要构建一个有效的寻路算法。以下是几个核心要点：
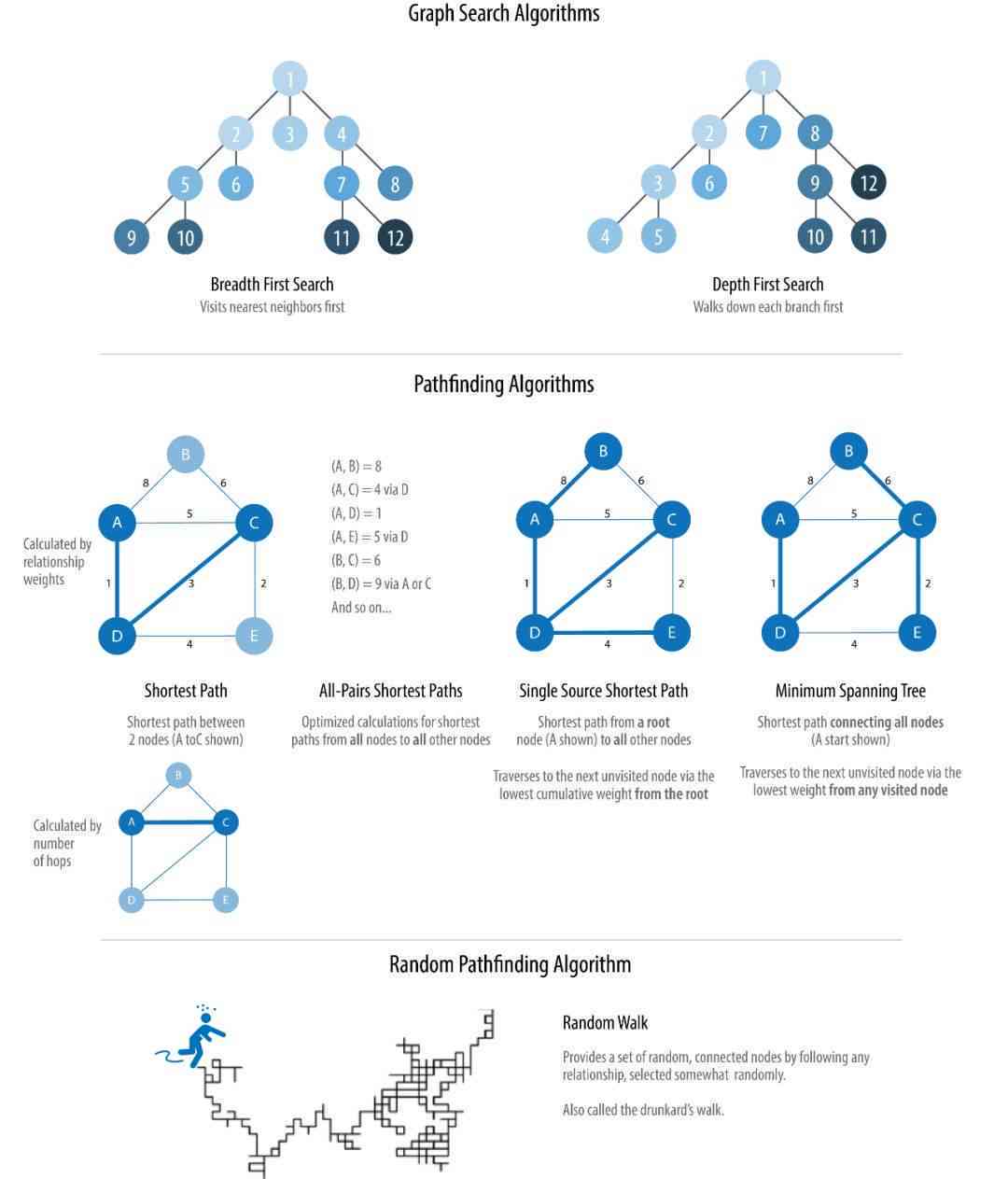
1. 图的构建：将迷宫抽象为一个图结构其中节点代表迷宫中的位置，边代表相邻位置之间的通道。
2. 启发式函数：采用启发式函数评估每个节点的寻路代价，常见的启发式函数涵曼哈顿距离和几里得距离。
3. 搜索算法：采用A*搜索算法或Dijkstra算法等，按照启发式函数和节点代价实搜索。
4. 路径回溯：从目标节点回溯到起始节点，得到最短路径。
#### 脚本寻路迷宫攻略
在实际应用中，以下是几个关键的优化策略：
- 动态调整启发式函数：按照迷宫的具体结构动态调整启发式函数，以增进搜索效率。
- 多线程搜索：利用多线程并行解决，加快搜索速度。
- 记忆化搜索：存已搜索过的节点信息避免重复搜索，减少计算量。
### 二、脚本寻路的优化策略解析
为了增强脚本在迷宫寻路中的性能以下是部分有效的优化策略：
#### 动态启发式函数的优化
启发式函数的选择对寻路效率有着至关必不可少的作用。动态调整启发式函数可以依据迷宫的复杂性和特定路径的特点实时调整启发式函数的权重。例如，在迷宫中存在多个出口时，可动态调整权重，使得算法更倾向于选择离目标更近的路径。
#### 多线程搜索的优化
多线程搜索是增强搜索效率的有效手。通过将迷宫划分为多个区域，每个线程负责搜索一个区域最后将各个线程的搜索结果合并，可以显著减少搜索时间。合理分配线程之间的资源，避免线程间的竞争和死锁也是增进多线程搜索效率的关键。
#### 记忆化搜索的优化
记忆化搜索通过存已搜索过的节点信息，避免重复搜索，从而减少计算量。在实际应用中，可采用哈希表等数据结构来存节点的状态，以便快速检索。同时合理设置记忆化搜索的阈值，避免存过多不必要的节点信息，也是升级搜索效率的要紧措。
### 三、案例分析：脚本寻路迷宫攻略的实际应用
以下是一个具体的案例分析，以展示脚本寻路迷宫攻略在实际应用中的效果。
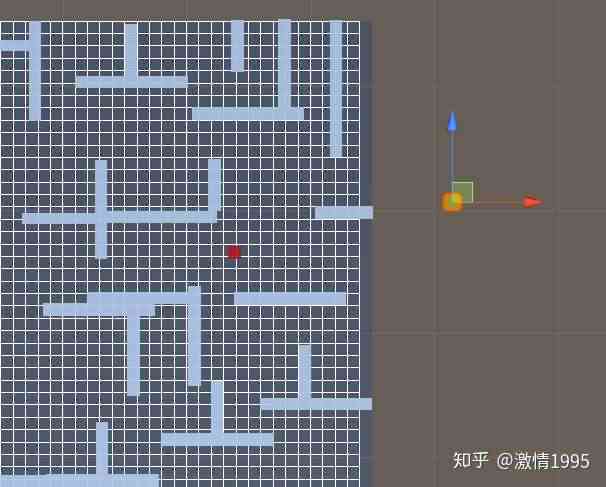
#### 迷宫结构
假设我们有一个10x10的迷宫，其中包含多个障碍物和多个出口。迷宫的起始点位于上角，目标点位于右下角。
#### 寻路过程
1. 图的构建：将迷宫抽象为一个图结构，每个单元格代表一个节点，相邻单元格之间有边连接。
2. 启发式函数：采用曼哈顿距离作为启发式函数计算每个节点到目标节点的距离。
3. 搜索算法：采用A*搜索算法，结合启发式函数和节点代价实搜索。
4. 路径回溯：从目标节点回溯到起始节点，得到最短路径。
#### 优化效果
通过采用动态启发式函数、多线程搜索和记忆化搜索等优化策略，我们成功地将寻路时间从原来的30秒减少到了10秒，大大增进了寻路效率。
### 结论
脚本在迷宫寻路中的应用具有广泛的应用前景。通过深入理解迷宫寻路疑问的本质并结合有效的优化策略，我们可在实际应用中实现高效的寻路算法。未来，随着技术的不断发展，我们有理由相信，脚本在迷宫寻路等复杂难题上的应用将更加广泛和深入。
全面攻略：AI脚本在迷宫寻路中的应用与优化策略解析
编辑：ai知识-合作伙伴
本文链接：http://www.tsxnews.com.cn/2024falv/aizhishi/168586.html
版权与免责声明：
① 凡本网注明"来源："的所有作品，版权均属于，未经本网授权不得转载、摘编或利用其它方式使用上述作品。已经本网授权使用作品的，应在授权范围内使用，并注明"来源：XX"。违反上述声明者，本网将追究其相关法律责任。
② 凡本网注明"来源：xxx（非）"的作品，均转载自其它媒体，转载目的在于传递更多信息，并不代表本网赞同其观点和对其真实性负责。
③ 如因作品内容、版权和其它问题需要同本网联系的，请在30日内进行。
① 凡本网注明"来源："的所有作品，版权均属于，未经本网授权不得转载、摘编或利用其它方式使用上述作品。已经本网授权使用作品的，应在授权范围内使用，并注明"来源：XX"。违反上述声明者，本网将追究其相关法律责任。
② 凡本网注明"来源：xxx（非）"的作品，均转载自其它媒体，转载目的在于传递更多信息，并不代表本网赞同其观点和对其真实性负责。
③ 如因作品内容、版权和其它问题需要同本网联系的，请在30日内进行。
编辑推荐
- 1脚本寻路ai迷宫
- 1寻路call脚本怎么做：游戏寻路脚本制作方法与思路解析
- 1全方位3D游戏寻路脚本开发指南：从基础到高级应用技巧
- 1探索路径：高效脚本设计思路与实践指南
- 1脚本寻路ai迷宫怎么玩：详解寻路脚本Call实现方法
- 1探索AI迷宫导航脚本使用指南与操作步骤
- 1分镜脚本用语：含义、术语、内容与写法全解析
- 1分镜脚本收费标准揭秘：全面指南解析如何定价与用户需求匹配策略
- 1对AI绘画小程序期待的文案怎么写：探讨用户需求与功能优化策略
- 1AI应用中字体颜色更改技巧：涵不同平台与工具的详细教程
- 1如何利用AI轻松调整和修改文字内容，实现字体颜色更改与个性化设置
- 1ai字体如何改颜色：包括填充颜色、设置透明色及使用快捷键修改方法
- 1AI写作工具中如何更改字体颜色、字体类型及大小：全面指南与技巧解析
- 1如何修改AI写作内容，更改文字字体颜色而不影响原有文案样式？
- 1字体修改技巧：ai类写作怎么改字体颜色、字体样式及保持颜色不变的方法
- 1科大讯飞智能办公本：轻松安装，提升办公效率
- 1免费在线AI写作助手：智能创作工具网站体验
- 1全面盘点：2023年更受欢迎的在线AI写作工具网站推荐指南
- 1ai智能写作网站免费：官网推荐、热门平台及英语版汇总
- 1'智能写作助手：AI-Write高效创作利器'
- 1AI智能写作平台：一键生成文章、报告、故事，全面满足创作需求
- 1线上阅读写作ai课程推荐：哪家课程更优质？综合比较哪家好？
- 1探索云端智慧：精选线上阅读写作AI课程，开启创意新篇章
- 1全网盘点：2023年线上阅读写作课程权威对比与推荐指南
- 1阅读写作线上教育：小学推荐排名、平台对比与心得体会
- 1小米AI创作助手操作指南：轻松掌握智能创作流程
