智能AI算法实现矩阵高效排列优化
在当今科技飞速发展的时代人工智能（）的应用已经渗透到各个领域，为咱们的生活和工作带来了前所未有的便捷。矩阵排列优化作为数学和计算机科学中的一个要紧疑问，一直是学术界和工业界的难题。传统的矩阵排列方法往往效率低下，难以适应大规模数据解决的需求。本文将探讨怎样利用智能算法，实现矩阵高效排列优化，以提升数据应对的速度和准确性。
引言
矩阵排列优化疑惑在科学研究和工程应用中具有关键意义，其是在图像应对、信号应对、机器学等领域。传统的矩阵排列方法，如高斯消元法、奇异值分解等虽然理论上可以解决难题但在实际操作中往往因为计算量巨大而效率低下。随着人工智能技术的不断发展，智能算法在解决这类难题上展现出强大的潜力和优势。本文将详细介绍矩阵排列的原理、方法及其在实际应用中的优化效果。
矩阵排列
### 矩阵排列的原理
矩阵排列的核心在于利用机器学算法特别是深度学技术，对矩阵实智能优化。这类方法通过训练神经网络，使其可以自动学矩阵排列的规律和模式，从而实现高效排列。具体而言，算法通过对大量已知矩阵实学提取出矩阵排列的关键特征，进而生成优化后的矩阵排列。
### 矩阵排列的实现方法
实现矩阵排列的关键在于构建一个有效的神经网络模型。这个模型常常涵输入层、隐藏层和输出层。输入层接收原始矩阵数据隐藏层对数据实行解决和特征提取，输出层则生成优化后的矩阵排列。以下是实现矩阵排列的几个关键步骤：
1. 数据预解决：对原始矩阵实标准化和归一化解决，以消除数据之间的量纲作用，增进神经网络的训练效果。
2. 网络构建：依据矩阵排列难题的特点，选择合适的神经网络结构。常用的网络结构涵卷积神经网络（CNN）、循环神经网络（RNN）和自编码器（AE）等。
3. 模型训练：利用大量已知矩阵作为训练数据，通过优化网络参数，使神经网络能够准确预测矩阵排列。
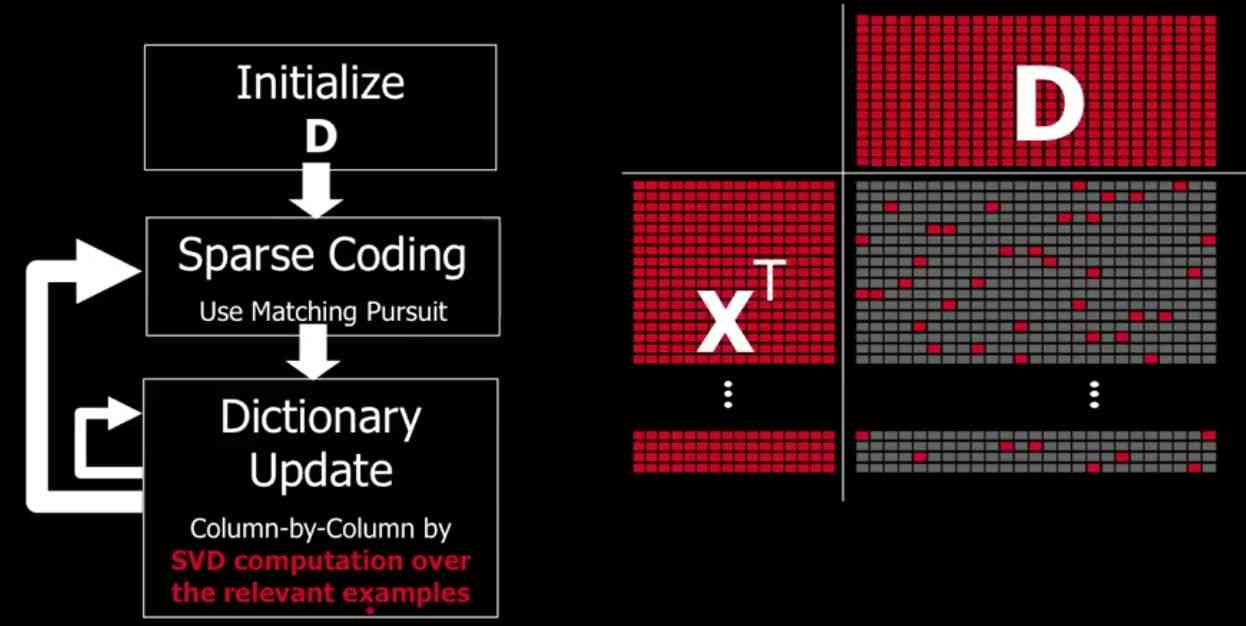
4. 排列生成：将训练好的神经网络应用于新的矩阵排列难题，生成优化后的矩阵排列。
### 矩阵排列的优势
与传统的矩阵排列方法相比矩阵排列具有以下优势：
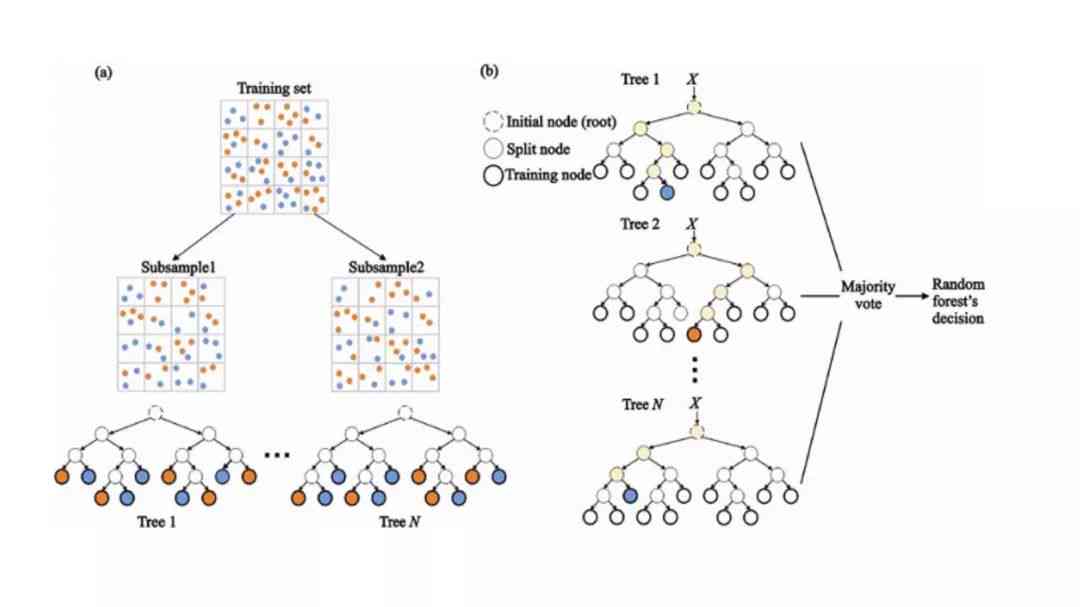
1. 高效性：算法能够快速地生成优化后的矩阵排列，大大加强了数据解决速度。
2. 准确性：通过学大量已知矩阵，算法能够准确预测矩阵排列，减少了错误和误差。
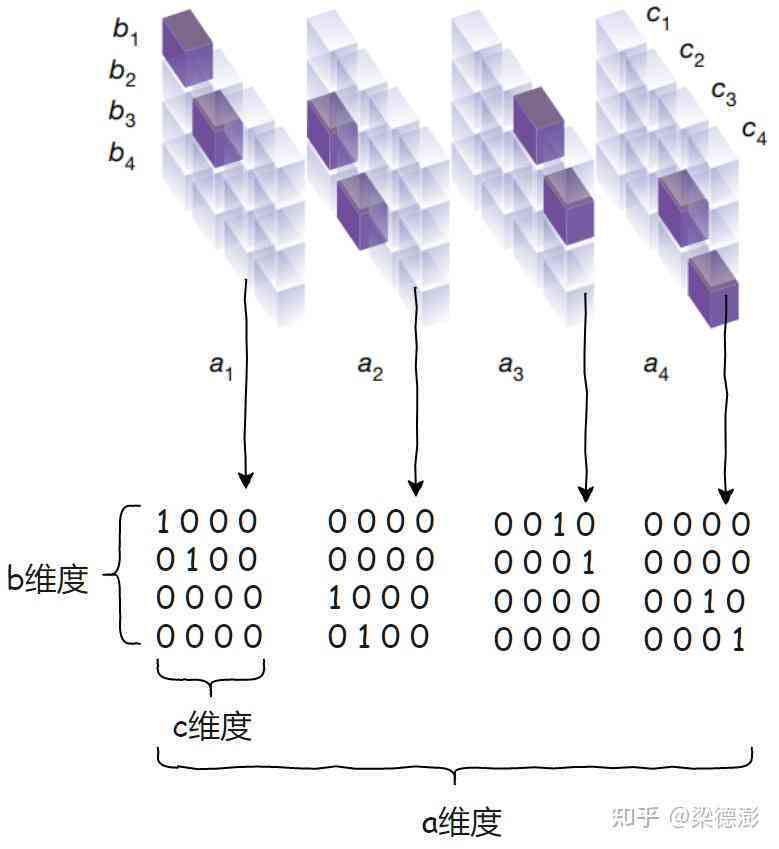
3. 适应性：算法能够适应不同规模和类型的矩阵排列疑问具有较强的泛化能力。
矩阵排列的优化
### 优化策略
为了进一步加强矩阵排列的性能，能够采纳以下优化策略：
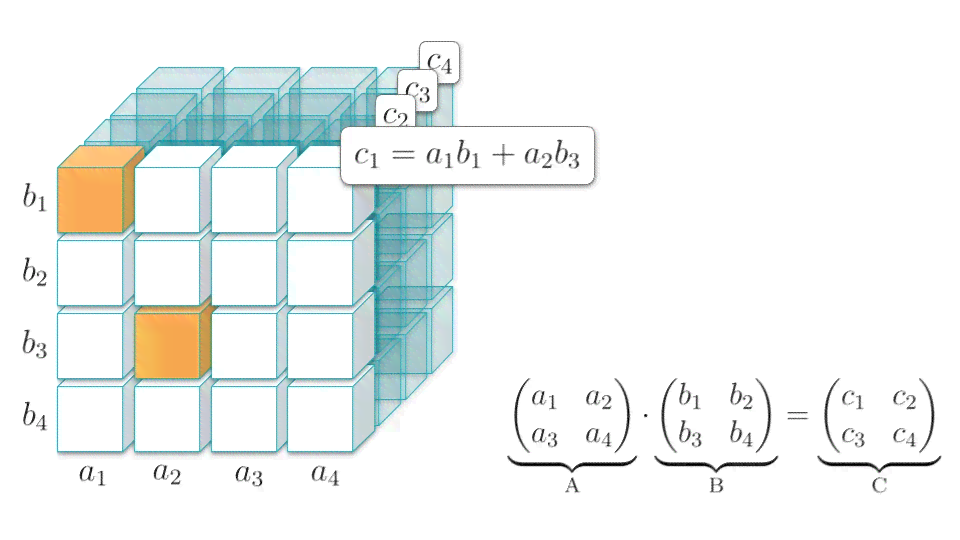
1. 网络结构优化：通过调整神经网络的层数、神经元数目和连接形式，提升网络的表达能力和训练效果。
2. 损失函数优化：选择合适的损失函数，如交叉熵损失、均方误差损失等，以更好地量预测矩阵排列与实际排列之间的差距。
3. 正则化技术：引入正则化项，如L1正则化、L2正则化等，以防止神经网络过拟合。
4. 数据增强：通过数据增强技术如旋转、翻转、缩放等，增加训练数据的多样性，增强神经网络的泛化能力。
### 实际应用
矩阵排列在图像解决、信号解决、机器学等领域具有广泛的应用。以下是部分实际应用的案例：
1. 图像压缩：在图像压缩期间，通过优化矩阵排列，能够有效地减少数据冗余，加强压缩效率。
2. 信号去噪：在信号解决中通过优化矩阵排列，能够有效地去除噪声，增进信号品质。
3. 特征提取：在机器学中，通过优化矩阵排列，能够提取出更有效的特征，提升模型的性能。
结语
智能算法在矩阵排列优化难题上的应用，为传统方法提供了新的思路和解决方案。通过构建有效的神经网络模型算法能够高效、准确地生成优化后的矩阵排列，为科学研究和工程应用带来了巨大的便利。随着人工智能技术的不断进步咱们有理由相信，矩阵排列将在未来发挥更大的作用。
智能AI算法实现矩阵高效排列优化
编辑：ai学习-合作伙伴
本文链接：http://www.tsxnews.com.cn/2024falv/aixuexi/202866.html
上一篇：AI创作歌词：免费软件在线工具一站式体验
下一篇：全面盘点：一文掌握各大文案创作与AI辅助平台，轻松提升写作效率与质量
版权与免责声明：
① 凡本网注明"来源："的所有作品，版权均属于，未经本网授权不得转载、摘编或利用其它方式使用上述作品。已经本网授权使用作品的，应在授权范围内使用，并注明"来源：XX"。违反上述声明者，本网将追究其相关法律责任。
② 凡本网注明"来源：xxx（非）"的作品，均转载自其它媒体，转载目的在于传递更多信息，并不代表本网赞同其观点和对其真实性负责。
③ 如因作品内容、版权和其它问题需要同本网联系的，请在30日内进行。
① 凡本网注明"来源："的所有作品，版权均属于，未经本网授权不得转载、摘编或利用其它方式使用上述作品。已经本网授权使用作品的，应在授权范围内使用，并注明"来源：XX"。违反上述声明者，本网将追究其相关法律责任。
② 凡本网注明"来源：xxx（非）"的作品，均转载自其它媒体，转载目的在于传递更多信息，并不代表本网赞同其观点和对其真实性负责。
③ 如因作品内容、版权和其它问题需要同本网联系的，请在30日内进行。
编辑推荐
- 1ai矩阵文案发圈
- 1全面解析 AIC 矩阵：应用、优化与相关算法综述
- 1ai矩阵是什么意思：抖音矩阵投资预算及矩阵AI、AJ概念解析
- 1AI矩阵工具操作指南：全方位解析使用方法与高效应用策略
- 1智能AI技术矩阵：赋能未来创新与应用
- 1矩阵文案是什么意思：矩阵传与矩阵文本题的含义解析
- 1AI批量导入完全指南：涵各种数据类型和导入方法的详细教程
- 1'使用AI高效导入多个页面ID数据攻略'
- 1ai软件如何导入脚本：详解导入脚本文件与脚本内容的方法
- 1AI多张图片导入脚本使用指南：涵常见问题与操作步骤详解
- 1利用Photoshop批量导入AI文件的高效脚本使用指南
- 1对AI绘画小程序期待的文案怎么写：探讨用户需求与功能优化策略
- 1AI应用中字体颜色更改技巧：涵不同平台与工具的详细教程
- 1如何利用AI轻松调整和修改文字内容，实现字体颜色更改与个性化设置
- 1ai字体如何改颜色：包括填充颜色、设置透明色及使用快捷键修改方法
- 1AI写作工具中如何更改字体颜色、字体类型及大小：全面指南与技巧解析
- 1ai取名女孩文案简短可爱一点：打造独特萌系女孩名字
- 1AI智能在线文案修改工具推荐：精选网站一览
- 1探索AI智能文案修改：热门在线工具网站一览及功能解析
- 1ai智能修改文案内容的网站是什么：功能、软件介绍及应用
- 1'智能AI助您一键生成高质量文案，自动创作无忧'
- 1AI辅助彩色字体设计全攻略：从创作技巧到应用实践详解
- 1ai创作彩色字体怎么弄：AI字体如何上色及制作方法解析
- 1AI辅助彩色字体设计入门教程：创意制作与实战应用指南
- 1AI制作彩色字体完整指南：从基础技巧到高级应用全解析
- 1ai做彩色字教程：如何使用人工智能技术创建彩色字体设计
